蜂の巣が六角形でできていることはみなさんよくご存知ですよね。円形ではどうしても隙間ができてしまいます。六角形なら平面をびっしり敷き詰めることができます。
では、正五角形で平面を敷き詰めることはできるでしょうか?
答えは、できない。まじめに考えれば、、、
科学者や技術者は、ときにまじめに考えてはいけないときがあります。
「平面にはできないけど、平面っぽくはできるんじゃねぇ?」
そう考えたらできちゃった、やっちゃったのが東北大学のこの研究成果です。
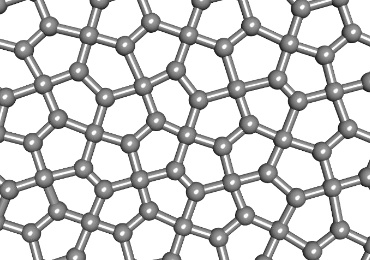
グラフェンとは、炭素が六角形セルで結合された平面シートのことです。まさに蜂の巣構造。平面としてはダイヤモンドより強く、熱伝導、電気伝導度がトップクラスの物質です。
幾何学的には平面を正五角形で敷き詰めることは不可能ですが、東北大学はわずかに立体的に配置することで平面的に敷き詰めることができることを発見しました。ペンタブラフェンと呼ばれています。
出典:東北大学プレスリリース
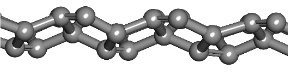
わずかに立体的と言っても、その厚みは0.6Å(オングストローム)。炭素結合の原子の直径の半分以下ですから、日常生活的には平面ですね。
エジプトのカイロの通りに五角形のみで構成されたタイルがあります。
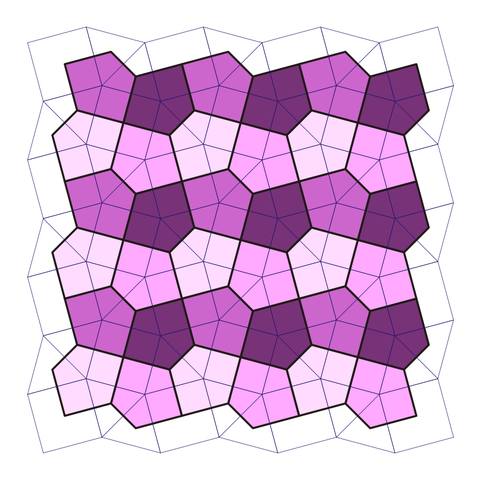
出典:Cairo pentagonal tiling(Author:TED-43)
よく見ると、五角形4つで六角形が構成されており、その六角形が敷き詰められています。ペンタグラフェンを上から見たものと非常によく似ています。
炭素を五角形の環でのみ敷き詰めたペンタグラフェンは、スーパーコンピューターの理論シミュレーションによれば次のような特徴があると予測されています。
1.透明半導体
2.負のポアソン比(押した方向と垂直方向にも縮む)
3.少量の電子追加で超伝導体に
4.ナノチューブを構成すればすべて半導体に
ただこれあくまで理論上の架空の物質なんです。ホントにできたらすごいことがたくさん起こります。理論的にできるとわかったので、実現に向けた科学技術の進歩スピードが一気に加速しますね。
- 投稿タグ
- 技術蓄積